Пятый постулат
Среди аксиом Евклида была аксиома о параллельности прямых, а точнее, пятый постулат о параллельных линиях: если две прямые образуют с третьей по одну ее сторону внутренние углы, сумма которых меньше развернутого угла, то такие прямые пересекаются при достаточном продолжении с одной стороны. В современной формулировке она говорит о существовании не более одной прямой, проходящей через данную точку вне данной прямой и параллельной этой данной прямой.
Сложность формулировки пятого постулата породила мысль о возможной зависимости его от других постулатов, и потому возникали попытки вывести его из остальных предпосылок геометрии. Как правило, это заканчивалось неудачей. Были попытки доказательства от противного: прийти к противоречию, предполагая верным отрицание постулата. Однако и этот путь был безуспешным.
Наконец, в начале XX века почти одновременно сразу у нескольких математиков: у К. Гаусса в Германии, у Я. Больяи в Венгрии и у Н. Лобачевского в России возникла мысль о существовании геометрии, в которой верна аксиома: на плоскости через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, не пересекающие данную.
В силу приоритета Н. Лобачевского, который первым выступил с этой идеей в 1826, и его вклада в развитие новой, отличной от евклидовой геометрии последняя была названа в его честь «геометрией Лобачевского».
Аксиоматика планиметрии Лобачевского отличается от аксиоматики планиметрии Евклида лишь одной аксиомой: аксиома параллельности заменяется на ее отрицание – аксиому параллельности Лобачевского

Найдутся такая прямая
Как уже отмечалось в § 15.1, непротиворечивость системы аксиом доказывается представлением модели, в которой реализуются данные аксиомы. Модель планиметрии Лобачевского на евклидовой плоскости, которая будет здесь представлена, сделана по материалам учебника «Геометрия» (А. Д. Александров, А. Л. Вернар, В. И. Рыжик, М: Просвещение, 1991). Эта модель была предложена французским математиком Анри Пуанкаре в 1882 году.
Для начала напомним основные понятия и аксиоматику, на которой базировалось изложение, систематизировав их заново и дополнив необходимыми аксиомами.
За основные объекты были приняты точка, прямая и фигура. За основные отношения между этими объектами принимаются:
1) точка принадлежит фигуре, в частности прямой;
2) точка лежит между двумя точками для точек прямой.
Следующие определения базируются на основных определениях.
- Фигура называется объединением некоторых данных фигур, если ей принадлежат все точки этих фигур, и никакие другие.
- Отрезком называется часть прямой, которая состоит из всех точек этой прямой, лежащих между двумя данными ее точками. Эти точки называются концами отрезка.
- Лучом
AB называется часть прямой, состоящая из всех ее точек, лежащих по ту же сторону от точкиA , что и точкаB . ТочкаA называется вершиной луча. - Углом называется фигура, которая состоит из точки – вершины угла и двух различных лучей, исходящих из этой точки, – сторон угла.
- Полуплоскостью, ограниченной прямой
a , называется фигура, обладающая следующими свойствами:- она не содержит прямую
a ; - если точки
A иB принадлежат полуплоскости, то отрезокAB не имеет общих точек сa ; - если же
A принадлежит полуплоскости, аB нет, то отрезокAB имеет общую точку с прямойa .
- она не содержит прямую
Приведем систему аксиом, обозначив римской цифрой номер группы, а арабской – номер аксиомы в группе.

I. Аксиомы связи прямой и точки.
- Существуют, по крайней мере, две точки.
- Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.
- Через любые две точки можно провести прямую и только одну.
- Из трех точек на прямой одна и только одна лежит между двумя другими.

II. Метрические аксиомы отрезка.
- Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
- На каждом луче от его начала можно отложить отрезок заданной длины и только один.

III. Аксиома непрерывности.
Пусть
A иB – любые две точки прямойa и пусть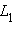 и
и 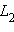 – совокупности всех точек отрезка
– совокупности всех точек отрезка AB , таких, что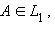
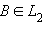 и любая точка из
и любая точка из 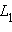 лежит по ту же сторону, что и точка
лежит по ту же сторону, что и точка A от любой точки из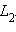 Тогда на прямой
Тогда на прямой a существует точкаC , такая, что любая точка из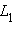 лежит по ту же сторону от
лежит по ту же сторону от C , что иA , а любая точка из – по ту же сторону от
– по ту же сторону от C , что иB .

IV. Аксиомы плоскости.
- Прямая разбивает плоскость на две полуплоскости.
- Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен 180°. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.
- От любого луча в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180°, и только один.
- Каков бы ни был треугольник, существует равный ему треугольник в заданном расположении относительно данного луча.

V. Аксиома параллельности Евклида.
Через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной.
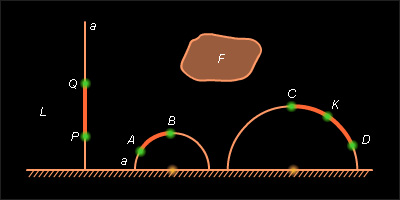
Построение модели Пуанкаре начнем с того, что придадим конкретный смысл основным объектам и основным отношениям планиметрии Лобачевского. Для этого фиксируем на евклидовской плоскости
Прямыми плоскости
Фигура на плоскости Лобачевского – это фигура полуплоскости
 |
| Рисунок 15.2.1 |
Неевклидовым движением называется преобразование
- Суперпозиция неевклидовых движений есть снова неевклидово движение. Это вытекает непосредственно из определения неевклидова движения.
- При неевклидовых движениях образами неевклидовых отрезков, прямых, лучей и углов являются соответственно неевклидовы отрезки, прямые, лучи и углы. Это свойство вытекает из свойств инверсии и свойств евклидовой осевой симметрии. Необходимо отметить, что неевклидовы углы, преобразующиеся друг в друга неевклидовым движением, равны в смысле приведенного ранее определения, и их величины (в евклидовом смысле) также равны.
- Если неевклидово движение переводит неевклидов луч в себя, то либо это тождественное преобразование, либо неевклидова осевая симметрия относительно неевклидовой прямой, содержащей данный луч. В обоих случаях все точки этой прямой для данного преобразования неподвижны. Это свойство дается без доказательства.
Выше дана реализация всех основных понятий аксиоматики планиметрии Лобачевского через понятия евклидовой геометрии. Теперь необходимо проверить справедливость приведенных выше аксиом.
Из группы аксиом I очевидна справедливость аксиом I.1, I.2, I.4.

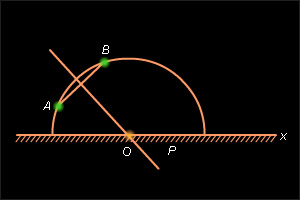
Пусть даны точки
 |
| Рисунок 15.2.2 |
Прямая (евклидова)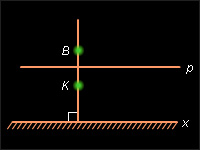
Рисунок 15.2.3 AB не перпендикулярна к абсолюту (рис. 15.2.2). Тогда серединный перпендикулярp отрезкаAB пересекает абсолют в некоторой точкеO . Так как по построениюOA =OB , то полуокружность окружностиS с центром в точкеO и радиусомOA , лежащая выше абсолюта, является неевклидовой прямой, содержащей точкиA иB . Эта прямая (неевклидова) единственна, так как на абсолюте есть лишь одна точка, равноудаленная от точекA иB , – это точкаO .- Прямая (евклидова)
AB перпендикулярна абсолюту (рис. 15.2.3). Тогда ее часть, лежащая выше абсолюта, будет неевклидовой прямой, проходящей через точкиA иB , посколькуp || x .

Так как каждый неевклидов отрезок
Для анализа второго случая допустим, что 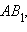 где
где 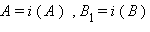 , а образом неевклидова отрезка – отрезок
, а образом неевклидова отрезка – отрезок 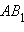 евклидова луча
евклидова луча 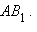 Здесь
Здесь 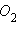 – вторая точка пересечения неевклидовой прямой
– вторая точка пересечения неевклидовой прямой 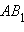 является образом отрезка
является образом отрезка 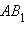 , то она выполнена и для неевклидова отрезка
, то она выполнена и для неевклидова отрезка
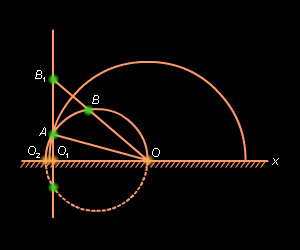 |
| Рисунок 15.2.4 |

Возможны несколько случаев.
- Пусть неевклидов луч представляет из себя луч евклидовой прямой, который не имеет точки пересечения с абсолютом (рис. 15.2.5). Тогда выполнение аксиомы следует из ее справедливости для евклидова луча.
Пусть неевклидов луч представляет из себя часть евклидовой прямой, перпендикулярной абсолюту и ограниченной началом
A луча (включая точкуA ) и точкойO , лежащей на абсолюте (рис. 15.2.6).
Рисунок 15.2.5 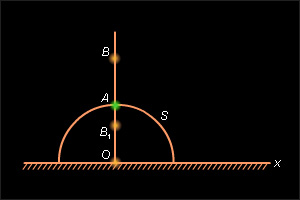
Рисунок 15.2.6 Сделаем преобразование инверсии относительно окружности
S с центром в точкеO и радиусомOA . По свойствам инверсии отрезокOA преобразуется в луч евклидовой прямойOA с началом в точкеA . В соответствии с аксиомой II.2 на полученном луче от его начала можно отложить отрезок заданной длины и только один. ПустьB – конец этого отрезка. Тогда ее прообразом при инверсииi является некоторая точка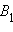 искомого евклидова луча. Так как отрезок
искомого евклидова луча. Так как отрезок 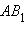 переводится в отрезок
переводится в отрезок AB неевклидовым движением, то они равны и равны их длины. Это завершает доказательство.Неевклидов луч – дуга
AO полуокружности, содержащая точкуA – начало луча, и не содержащая точкуO , точку пересечения полуокружности с абсолютом (рис. 15.2.7). Как и в случае рассмотрения аксиомы II.1, сделаем преобразование инверсииi относительно окружностиS с центром в точкеO и радиусомAO . Образом неевклидова лучаAO будет луч евклидовой прямой, перпендикулярной абсолюту. На этом луче можно отложить отрезок данной длины и только один. ПустьB – конец этого отрезка. Далее обоснование дословно повторяет обоснование, приведенное в предыдущем пункте.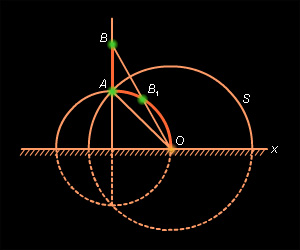
Рисунок 15.2.7
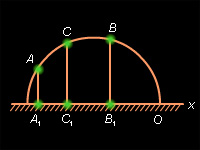 |
| Рисунок 15.2.8 |
Аксиома непрерывности III для неевклидовых отрезков сводится к случаю евклидовых отрезков проектированием на абсолют (рис. 15.2.8) или преобразованием неевклидова отрезка в отрезок евклидовой прямой, перпендикулярной абсолюту, с помощью инверсии, описанной при доказательстве справедливости аксиомы II.1. В модели Пуанкаре выполняется аксиома IV.1. Неевклидовы полуплоскости изображены на рис. 15.2.9. Неевклидов отрезок, соединяющий две точки неевклидовой полуплоскости, не пересекает ее границы. Действительно, предположив противное, мы пришли бы к тому, что евклидовы окружности пересекались бы в четырех точках (рис. 15.2.10), что невозможно.
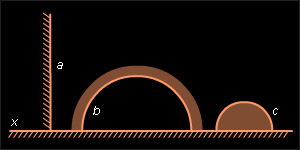 |
| Рисунок 15.2.9 |
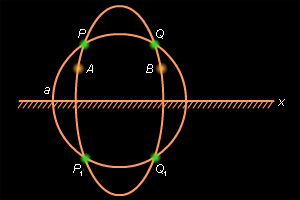 |
| Рисунок 15.2.10 |