Вход / Регистрация
12.02.2026, 13:52
Как часто во Вселенной появляется жизнь?
С 1960-х годов уравнение Дрейка используется для оценки того, сколько в галактике Млечный Путь существует разумных и способных к контакту внеземных цивилизаций. Следуя проторенному пути, новая формула оценивает частоту, с которой жизнь возникает на планете. Она может помочь нам выяснить, насколько в принципе вероятно возникновение жизни во Вселенной.
Новое уравнение, разработанное Кэлебом Шарвом из Колумбийского астробиологического центра и Лероем Кронином из Школы химии при Университете Глазго, пока не может оценить шансы на появление жизни где угодно, но обещает интересные перспективы в этом направлении.
Ученые надеются, что их новая формула, описанная в последнем издании Трудов Национальной академии наук (PNAS), воодушевит ученых на исследование различных факторов, которые связывают события возникновения жизни с особыми свойствами планетарной среды. В более широком смысле, они рассчитывают, что их уравнение будет в конечном счете использоваться для прогнозирования частоты возникновения жизни на планете, процесса также известного как абиогенеза.
Те, кто знаком с уравнением Дрейка, поймут и новое уравнение. Еще в 1961 году астроном Фрэнк Дрейк вывел вероятностную формулу, которая могла помочь прикинуть количество активных внеземных цивилизаций, передающих сигналы в радиодиапазоне в нашей галактике. Его формула содержала несколько неизвестных значений, включая среднюю скорость образования звезд, среднее число планет, которые могут потенциально поддерживать жизнь, долю планет, которым удалось обзавестись действительно разумной жизнью и так далее. У нас нет окончательного варианта уравнения Дрейка, но мы верим, что с каждым годом оно позволяет нам все точнее оценить неизвестно.
Новая формула, разработанная Шарфом и Кронином, не ставит перед собой задачу заменить уравнение Дрейка. Вместо этого она глубже погружает нас в статистику абиогенеза.
Вот так она выглядит:
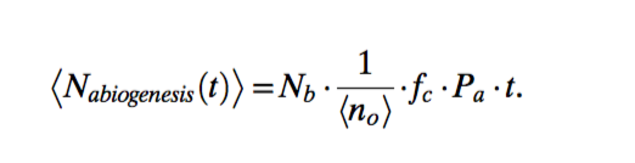
Где:
Nabiogenesis (t) = вероятность события возникновения жизни (абиогенеза)
Nb = число потенциальных строительных блоков
No = среднее число строительных блоков на организм, или биохимически значимую систему
fc = фракционная доступность строительных блоков в течение времени t
Pa = вероятность сборки за единицу времени
Выглядит сложно, но на деле все куда проще. Уравнение, если коротко, гласит, что вероятность возникновения жизни на планете тесно связана с количеством химических «строительных блоков», поддерживающих жизнь и доступных на планете.
Под строительными блоками ученые имеют в виду необходимый химический минимум для запуска процесса создания простых жизнеформ. Это могут быть основные пары ДНК/РНК или аминокислот, либо любые доступные молекулы или материалы на планете, которые могут участвовать в химических реакциях, приводящих к появлению жизни. Химия остается химией по всей Вселенной, но разные планеты могут создавать разные условия, пригодные для появления жизни.
Если более конкретно, уравнение Шарфа и Кронина утверждает, что шансы возникновения жизни на планете зависят от количества строительных блоков, которые могли бы существовать теоретически, количества доступных строительных блоков, вероятности того, что эти строительные блоки действительно станут жизнью (в процессе сборки), и количества строительных блоков, необходимых для производства определенной формы жизни. В дополнение к определению химических предпосылок для возникновения жизни, это уравнение стремится определить частоту, с которой возникают репродуктивные молекулы. У нас на Земле абиогенез состоялся в тот момент, когда появилась РНК. За этим важнейшим шагом последовал расцвет простой одноклеточной жизни (прокариот) и сложной одноклеточной жизни (эукариот).
«Наш подход связывает химию на планете с глобальным темпом зарождения жизни — это важно, поскольку мы начинаем находить много солнечных систем с кучей планет, — рассказал Кронин. — Например, мы считаем, что присутствие небольшой планеты поблизости — вроде Марса — может быть важным, поскольку она остыла быстрее Земли… часть химических процессов могла начаться, а после передать сложную химию на землю, чтобы помочь «подтолкнуть» химию на земле».
Одно из важных следствий этого исследования в том, что планеты нельзя изучать изолировано. Как сказал Кронин, Марс и Земля могли быть вовлечены в обмен химическими веществами однажды в далеком прошлом — и этот обмен веществами мог послужить началу жизни на Земле. Возможно, обмен химическими строительными блоками между близко расположенными планетами может существенно увеличить шансы на появление на них жизни.
Так сколько же примеров жизни таит в себе Вселенная?
«Это сложный вопрос, — говорит Кронин. — Из нашей работы следует, что солнечные системы с несколькими планетами могут быть прекрасными кандидатами для более внимательного исследования — что нам стоит сосредоточиться на многопланетных системах и поискать в них жизнь». Каким образом? Стоит искать признаки изменения атмосфер, сложной химии, наличия сложных соединений и вариаций в климате, которые могут быть обусловлены биологической жизнью.
У нас нет достаточного количества эмпирических данных, чтобы закончить уравнение Шарфа и Кронина в данный момент, но в будущем это изменится. В ближайшем десятилетии мы сможем использовать телескоп Джеймса Вебба и миссию MIT Tess, чтобы восполнить недостающие значения. В конце концов, мы найдем ответ на этот волнующий нас вопрос.
Новое уравнение, разработанное Кэлебом Шарвом из Колумбийского астробиологического центра и Лероем Кронином из Школы химии при Университете Глазго, пока не может оценить шансы на появление жизни где угодно, но обещает интересные перспективы в этом направлении.
Ученые надеются, что их новая формула, описанная в последнем издании Трудов Национальной академии наук (PNAS), воодушевит ученых на исследование различных факторов, которые связывают события возникновения жизни с особыми свойствами планетарной среды. В более широком смысле, они рассчитывают, что их уравнение будет в конечном счете использоваться для прогнозирования частоты возникновения жизни на планете, процесса также известного как абиогенеза.
Те, кто знаком с уравнением Дрейка, поймут и новое уравнение. Еще в 1961 году астроном Фрэнк Дрейк вывел вероятностную формулу, которая могла помочь прикинуть количество активных внеземных цивилизаций, передающих сигналы в радиодиапазоне в нашей галактике. Его формула содержала несколько неизвестных значений, включая среднюю скорость образования звезд, среднее число планет, которые могут потенциально поддерживать жизнь, долю планет, которым удалось обзавестись действительно разумной жизнью и так далее. У нас нет окончательного варианта уравнения Дрейка, но мы верим, что с каждым годом оно позволяет нам все точнее оценить неизвестно.
Новая формула, разработанная Шарфом и Кронином, не ставит перед собой задачу заменить уравнение Дрейка. Вместо этого она глубже погружает нас в статистику абиогенеза.
Вот так она выглядит:
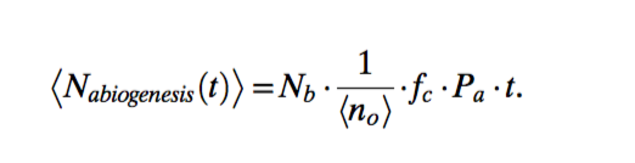
Где:
Nabiogenesis (t) = вероятность события возникновения жизни (абиогенеза)
Nb = число потенциальных строительных блоков
No = среднее число строительных блоков на организм, или биохимически значимую систему
fc = фракционная доступность строительных блоков в течение времени t
Pa = вероятность сборки за единицу времени
Выглядит сложно, но на деле все куда проще. Уравнение, если коротко, гласит, что вероятность возникновения жизни на планете тесно связана с количеством химических «строительных блоков», поддерживающих жизнь и доступных на планете.
Под строительными блоками ученые имеют в виду необходимый химический минимум для запуска процесса создания простых жизнеформ. Это могут быть основные пары ДНК/РНК или аминокислот, либо любые доступные молекулы или материалы на планете, которые могут участвовать в химических реакциях, приводящих к появлению жизни. Химия остается химией по всей Вселенной, но разные планеты могут создавать разные условия, пригодные для появления жизни.
Если более конкретно, уравнение Шарфа и Кронина утверждает, что шансы возникновения жизни на планете зависят от количества строительных блоков, которые могли бы существовать теоретически, количества доступных строительных блоков, вероятности того, что эти строительные блоки действительно станут жизнью (в процессе сборки), и количества строительных блоков, необходимых для производства определенной формы жизни. В дополнение к определению химических предпосылок для возникновения жизни, это уравнение стремится определить частоту, с которой возникают репродуктивные молекулы. У нас на Земле абиогенез состоялся в тот момент, когда появилась РНК. За этим важнейшим шагом последовал расцвет простой одноклеточной жизни (прокариот) и сложной одноклеточной жизни (эукариот).
«Наш подход связывает химию на планете с глобальным темпом зарождения жизни — это важно, поскольку мы начинаем находить много солнечных систем с кучей планет, — рассказал Кронин. — Например, мы считаем, что присутствие небольшой планеты поблизости — вроде Марса — может быть важным, поскольку она остыла быстрее Земли… часть химических процессов могла начаться, а после передать сложную химию на землю, чтобы помочь «подтолкнуть» химию на земле».
Одно из важных следствий этого исследования в том, что планеты нельзя изучать изолировано. Как сказал Кронин, Марс и Земля могли быть вовлечены в обмен химическими веществами однажды в далеком прошлом — и этот обмен веществами мог послужить началу жизни на Земле. Возможно, обмен химическими строительными блоками между близко расположенными планетами может существенно увеличить шансы на появление на них жизни.
Так сколько же примеров жизни таит в себе Вселенная?
«Это сложный вопрос, — говорит Кронин. — Из нашей работы следует, что солнечные системы с несколькими планетами могут быть прекрасными кандидатами для более внимательного исследования — что нам стоит сосредоточиться на многопланетных системах и поискать в них жизнь». Каким образом? Стоит искать признаки изменения атмосфер, сложной химии, наличия сложных соединений и вариаций в климате, которые могут быть обусловлены биологической жизнью.
У нас нет достаточного количества эмпирических данных, чтобы закончить уравнение Шарфа и Кронина в данный момент, но в будущем это изменится. В ближайшем десятилетии мы сможем использовать телескоп Джеймса Вебба и миссию MIT Tess, чтобы восполнить недостающие значения. В конце концов, мы найдем ответ на этот волнующий нас вопрос.



