Вход / Регистрация
13.03.2026, 20:55
На что будут способны ДНК-компьютеры будущего?
Согласно прогнозу агентства IDC, к 2020 году объем данных, созданных и сохраненных человечеством, достигнет 40 000 эксабайт. Это 40 трлн гигабайт, или 5200 гигабайт на душу населения. Для хранения всей этой информации было бы достаточно менее 100 г ДНК. Сей факт заставляет искренне верить в перспективу развития ДНК-компьютеров.
Упаковка равных по массе контейнеров, поиск кратчайшего маршрута между несколькими пунктами назначения, расшифровка закодированных данных — что может быть общего у этих задач? Ответ прост — они слишком сложны для современных компьютеров.
Классическим примером может служить старинная задача о Кенигсбергских мостах, в которой спрашивалось, как пройти по всем семи мостам города, не пройдя ни по одному из них дважды. Впервые задача была решена в 1736 году великим Леонардом Эйлером, который родился в Швейцарии, но практически полжизни жил и работал в России, в Петербургской академии наук. Эйлер хорошо знал русский язык и многие свои труды публиковал на русском.
Работы Эйлера заложили основы теории графов, позволяющей формализовать подобные задачи. Точки маршрута (берега) в ней называются вершинами графа, переходы между вершинами (мосты) — ребрами. Каждое ребро имеет вес, характеризующий сложность данного перехода (расстояние, которое необходимо пройти). Эйлер выяснил, что пройти по каждому мосту Кенигсберга лишь по одному разу невозможно. Но это не отменяет другой, более важной задачи: как обойти все мосты города кратчайшим путем (задача коммивояжера)? Сложность этой и подобных задач заключается в том, что на сегодняшний день не существует ни одного известного алгоритма их решения, кроме полного перебора вариантов. В каждой последующей вершине графа задача распадается на множество аналогичных задач, и количество возможных решений возрастает экспоненциально.
Упаковка равных по массе контейнеров, поиск кратчайшего маршрута между несколькими пунктами назначения, расшифровка закодированных данных — что может быть общего у этих задач? Ответ прост — они слишком сложны для современных компьютеров.
Классическим примером может служить старинная задача о Кенигсбергских мостах, в которой спрашивалось, как пройти по всем семи мостам города, не пройдя ни по одному из них дважды. Впервые задача была решена в 1736 году великим Леонардом Эйлером, который родился в Швейцарии, но практически полжизни жил и работал в России, в Петербургской академии наук. Эйлер хорошо знал русский язык и многие свои труды публиковал на русском.
Работы Эйлера заложили основы теории графов, позволяющей формализовать подобные задачи. Точки маршрута (берега) в ней называются вершинами графа, переходы между вершинами (мосты) — ребрами. Каждое ребро имеет вес, характеризующий сложность данного перехода (расстояние, которое необходимо пройти). Эйлер выяснил, что пройти по каждому мосту Кенигсберга лишь по одному разу невозможно. Но это не отменяет другой, более важной задачи: как обойти все мосты города кратчайшим путем (задача коммивояжера)? Сложность этой и подобных задач заключается в том, что на сегодняшний день не существует ни одного известного алгоритма их решения, кроме полного перебора вариантов. В каждой последующей вершине графа задача распадается на множество аналогичных задач, и количество возможных решений возрастает экспоненциально.

В современных лабораториях процесс создания коротких фрагментов ДНК с заданным кодом полностью автоматизирован. Небольшие науч-ные группы, которые не могут позволить себе собственный синтезатор, заказывают олигонуклеотиды у коммерческих фирм.
В основе кремниевых компьютеров лежит последовательный принцип решения задач. Один за другим компьютер складывает возможные маршруты, проверяет их соответствие условиям задачи, вычисляет их длину, сравнивает результаты и выявляет кратчайший путь. Для решения задачи с 30 мостами наиболее прямолинейным способом, именуемым методом лексического перебора, понадобилось бы время большее, чем возраст Вселенной.
К счастью, существуют алгоритмы, позволяющие кремниевым компьютерам решать относительно сложные комбинаторные задачи за приемлемое время. Но есть и другой путь — вычисления с высокой параллельностью, позволяющие анализировать все возможные решения задачи одновременно. Именно этим и займутся будущие ДНК-компьютеры.
К счастью, существуют алгоритмы, позволяющие кремниевым компьютерам решать относительно сложные комбинаторные задачи за приемлемое время. Но есть и другой путь — вычисления с высокой параллельностью, позволяющие анализировать все возможные решения задачи одновременно. Именно этим и займутся будущие ДНК-компьютеры.
Биоавтомат
Интересно, что создатель первого ДНК-компьютера Леонард Адлеман известен прежде всего как выдающийся криптограф. В названии алгоритма шифрования RSA, без которого немыслимы мировые финансы, третья буква обозначает именно его фамилию (Rivest — Shamir — Adleman).
В 1994 году Адлеман повторил опыт Эйлера, предложив собственное решение задачи коммивояжера для графа с семью вершинами. В этом ему помог не привычный кусок кремния, а несколько пробирок, каждая из которых содержала миллиарды миллиардов молекул ДНК — биологических нанокомпьютеров. Еще в далеком 1953 году нобелевские лауреаты Фрэнсис Крик, Джеймс Уотсон и Морис Уилкинс, расшифровавшие структуру ДНК, сравнивали эту молекулу с машиной Тьюринга, гипотетическим предвестником современных процессоров.

Двойная спираль ДНК — это не что иное, как программный код, общий для всех живых организмов на Земле. По простоте и универсальности он стоит на одной ступени с машинным двоичным кодом.
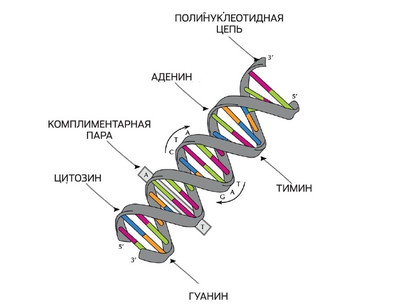
Напомним, что ДНК представляет собой две спирали, соединенные между собой парами азотистых оснований. Спирали — это гигантские макромолекулы, состоящие из дезоксирибозы и фосфатных групп. Если провести аналогию с машиной Тьюринга, спираль — это перфолента, на которой записан программный код.
Код состоит из четырех букв, обозначающих азотистые основания: А — аденин, Т — тимин, С — цитозин и G — гуанин. Азотистые основания двух соседних спиралей притягиваются друг к другу, причем аденин соединяется только с тимином, а цитозин — с гуанином. Благодаря азотистым основаниям две спирали, являющиеся зеркальным отображением друг друга, соединяются в одну молекулу ДНК.
ДНК в живом организме постоянно тиражируется с помощью молекулярных машин — энзимов. Хеликазы расщепляют двойную спираль на две комплементарные спирали. Полимераза, двигаясь вдоль одинарной спирали, выстраивает ее «зеркальную» копию. Такая копия называется дополнением Уотсона-Крика.
Код состоит из четырех букв, обозначающих азотистые основания: А — аденин, Т — тимин, С — цитозин и G — гуанин. Азотистые основания двух соседних спиралей притягиваются друг к другу, причем аденин соединяется только с тимином, а цитозин — с гуанином. Благодаря азотистым основаниям две спирали, являющиеся зеркальным отображением друг друга, соединяются в одну молекулу ДНК.
ДНК в живом организме постоянно тиражируется с помощью молекулярных машин — энзимов. Хеликазы расщепляют двойную спираль на две комплементарные спирали. Полимераза, двигаясь вдоль одинарной спирали, выстраивает ее «зеркальную» копию. Такая копия называется дополнением Уотсона-Крика.
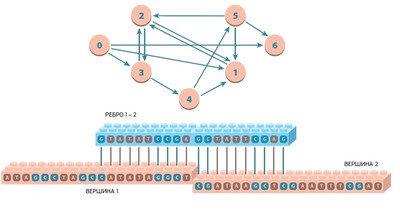
Принципиальная схема работы вычислительных блоков ДНК. В таком виде граф задачи был представлен в работе Леонарда Адлемана. Как видно из графа, для работы ДНК-компьютера ученому пришлось секвенировать 20 олигонуклеотидов, 7 из которых представляют вершины и 13 — ребра.
Абстрактная вычислительная машина, описанная в 1936 году Аланом Тьюрингом, представляла собой бесконечную ленту, поделенную на кадры с входящими данными, и управляющее устройство, движущееся вдоль ленты, считывающее данные и изменяющее свое состояние согласно некому внутреннему алгоритму. Чем не ДНК и полимераза?
Суп из кубиков LEGO
Чтобы решить задачу для графа с семью вершинами, Адлеман использовал простейший экстенсивный алгоритм: сгенерировать все возможные маршруты; исключить все пути, которые не проходят через заданные начальную и конечную точки; исключить все пути, которые проходят более семи вершин; исключить все пути, которые проходят более одного раза через одну вершину. ДНК-компьютер чем-то напоминает конструктор LEGO. Представьте себе, что есть кубики, обозначающие вершины графа, и перемычки, способные соединять вершины в цепочки любой длины.
В компьютере Адлемана каждый кубик представлял собой фрагмент ДНК с 20 азотистыми основаниями. Такие короткие отрезки ДНК называются олигонуклеотидами и кодируются с помощью олигонуклеотидного синтеза. Этот процесс давно отработан и поставлен на поток. Существуют даже коммерческие фирмы, которые за считаные часы могут синтезировать и прислать олигонуклеотиды с нужными кодами. А «20-битных» кубиков вполне достаточно для обозначения семи вершин графа.
Отдельный комплект олигонуклеотидов представляет ребра графа. Код ребра составляется из половинок кодов вершин, которые он соединяет, в «зеркальном» отображении. К примеру, для вершин ААСС и TTGG нужно сделать «перемычку» CCTT и «перевернуть» ее в GGAA. Тогда, встретившись в растворе, эти три олигонуклеотида соединятся в единый «отрезок пути», образовав двойную спираль.
Если смешать в пробирке миллиарды 20-буквенных «вершин» и миллиарды 20-буквенных «ребер», они соединятся в более длинные молекулы самыми разными способами. С большой вероятностью в пробирке будут одновременно находиться ДНК, кодирующие все возможные варианты пути через граф. Смешивать олигонуклеотиды нужно при определенных условиях, с добавлением лигазы — фермента, склеивающего разрывы в спиралях ДНК.
На следующем этапе необходимо отыскать цепочки, проходящие через заданные начальную и конечную точки. В этом поможет широко используемый в микробиологии и медицине метод полимеразной цепной реакции (ПЦР). В раствор, содержащий исходные молекулы, добавляются необходимые строительные материалы для ДНК (дезоксирибоза, фосфаты, азотистые основания), полимераза, а также молекулы «зацепок». «Зацепками» в нашем случае служат отрезки, кодирующие начальную и конечную вершины.
Раствор попеременно нагревается и охлаждается. При нагревании исходные ДНК распадаются на две спирали, а при охлаждении нужные нам спирали сначала рекомбинируют с «зацепками», а затем достраиваются полимеразой до своих точных копий. В результате нужных ДНК становится так много, что ненужными можно смело пренебречь.
На третьем этапе необходимо выделить лишь те молекулы, длина которых составляет ровно 140 оснований (семь раз по 20). Для этого применяется гель-электрофорез. ДНК помещаются в гелеобразный раствор и подвергаются воздействию электричества. Молекулы разной длины движутся в электрическом поле с разной скоростью и выстраиваются «по росту». Под микроскопом их можно различить даже визуально.
Четвертый этап позволяет выделить цепочки, содержащие все вершины. К отрезку ДНК, кодирующему определенную вершину, можно прикрепить крохотный кусочек металла. Этот отрезок легко соединится с молекулой, содержащей соответствующую вершину. С помощью магнита все такие молекулы можно отделить от остальных. Данную операцию повторяют для каждой вершины.
На пятом этапе достаточно применить метод ПЦР к тому, что осталось в пробирке, и отправить результат на секвенирование — процесс расшифровки ДНК, получивший широкое распространение в современной микробиологии. Если при секвенировании искомого пути не обнаружилось, значит, задача не имеет решения. К этому выводу и пришел Леонард Адлеман. Ведь задача о Кенигсбергских мостах не имеет решения, что доказал почти три века назад Леонард Эйлер.
И все-таки он танцует!
Ряд исследователей продолжили изыскания Адлемана, в частности, предложив кодировать веса ребер с помощью многократного повторения 20-значного кода. Таким образом, ребра с весом «пять» в пять раз длиннее ребер с весом «один», но при этом соединяются с теми же самыми вершинами.
Используя данный метод, можно найти кратчайший путь по графу с заданным количеством вершин. Необходимо сначала отобрать цепочки, проходящие через все вершины, с помощью магнитной сортировки, а затем применить гель-электрофорез, чтобы найти кратчайший путь.
В 1994 году Адлеман потратил на все описанные операции семь рабочих дней, в то время как самый обычный компьютер решил бы задачу перебором за считаные секунды. Сам ученый прокомментировал сей факт следующим образом: «Чудо не в том, что медведь танцует хорошо, а в том, что он вообще танцует». Адлеман доказал, что ДНК вполне способны на параллельные вычисления, и вопрос лишь в том, как сделать молекулярные вычисления удобными и технологичными.
В конце концов, если число вершин (городов, единиц груза, множителей шифра) увеличить хотя бы до пятидесяти, то кремниевый процессор спасует, тогда как ДНК-компьютер, возможно, только расправит плечи и вдохнет полной грудью.