Лента Мебиуса

30.07.11 Пожалуй, самую первую необычную фигуру придумал в середине ХIX столетия Август Мёбиус. Это был так называемый «лист Мёбиуса», или «лента Мёбиуса» – весьма простая и в то же время весьма странная конструкция.

Легко убедиться, что у этой фигуры всего одна поверхность!

Представьте себе что, например, по ленте Мёбиуса бежит муравей. Впрочем, поступим проще: посмотрим на ленту Мёбиуса, изображенную на хорошо известном рисунке Мориса Эшера.

Сделав круг, муравей прибегает к тому же месту, откуда он начал движение, но при этом оказывается с противоположной стороны плоской ленты! Естественно, пробежав еще один круг, он вернется в точку старта. (Конечно же, предполагается, что муравей не может перебраться через край ленты.)



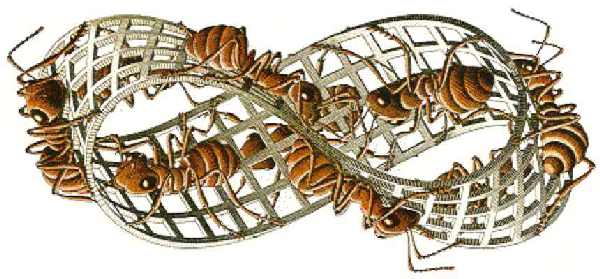
Сделав круг, муравей прибегает к тому же месту, откуда он начал движение, но при этом оказывается с противоположной стороны плоской ленты! Естественно, пробежав еще один круг, он вернется в точку старта. (Конечно же, предполагается, что муравей не может перебраться через край ленты.)




Немецкий геометр и астроном, профессор Лейпцигского университета. Основные труды по геометрии. Впервые ввел в проективную геометрию систему координат и аналитические методы исследования, получил новую классификацию кривых и поверхностей, установил общее понятие проективного преобразования, исследовал коррелятивные преобразования. Впервые установил существование односторонних поверхностей.

Ходит молва, что Мёбиусу пришла в голову идея об этой необычной геометрической фигуре, когда он увидел горничную, неправильно повязавшую свой шейный платок. Ну, что же, может быть, может быть! Ведь Исаак Ньютон тоже тянул с открытием всемирного закона тяготения, пока ему на голову не свалилось яблоко.
Справедливости ради, надо заметить, что сама фигура, называемая всеми лентой Мёбиуса, одновременно и независимо в том же 1858 году была построена и другим немецкими математиком Иоганном Бенедиктом Листингом (1808-1882), который, кстати, пустил в математический обиход и термин «топология».

Лента Мёбиуса сразу же привлекла внимание математиков. Одной из любопытных задач является следующая: какой длины (при заданной ширине) должна быть полосочка, чтобы ее можно было свернуть в лист Мёбиуса? Очень важный практический вопрос, неправда ли?

Но дело не ограничивается простой «классической» лентой Мёбиуса. Склейте ленту Мёбиуса из широкой полоски бумаги и попробуйте разрезать ее вдоль по средней линии. Начальная фаза разрезания показана на левом рисунке. А когда вы разрежете это кольцо до конца, то … увидите опять ленту Мёбиуса, правда, более «завинченную» (правый рисунок). Но муравей, начавши ползти опять пробежит по обеим сторонам полоски и вернется в точку старта.


Кстати, фокусники, разрезающие на удивление зрителей ленту Мёбиуса, называют получившуюся в результате фигуру почему-то «афганской лентой». Но не думайте, что на этом чудеса с лентой Мёбиуса закончились. А что получится, если полоску повернуть несколько раз перед склеиванием?

Все зависит от того, насколько закручена лента. При одном скручивании от простого кольца мы переходим к лента Мёбиуса.

 

 

Ну, а что же получится при двойном повороте ленты перед склеиванием? Оказывается, что в этом случае получается просто «закрученное» кольцо. Но если ленту повернуть перед склеиванием еще раз в том же направлении. То опять получится лента Мёбиуса, но уже «закрученная»!

 

Для удобства объяснения сути производимых операций выбрана лента, одна сторона которой белая, а вторая – серая. Тогда совершенно понятно, что сколько бы мы раз ни скручивали ленту, если окажется что ее так, что на стыке «встретились стороны с одним и тем же цветом, то это означает, что у склеенной ленты будет две поверхности – одна белая, а другая серая, т.е. будет образовано кольцо с винтообразной образующей лентой. Если же на стыке при склеивании серая сторона «встретится с белой, то после склеивания мы получим уже ленту Мёбиуса, хотя и тоже замысловатую. У нее будет всего одна поверхность: ведь Эшеровский муравей бегая по белой стороне, добегает в конце концов до границы, где начинается серая сторона и продолжает бежать уже по ней.

Интересны и свойства цепей, образованных плоскими кольцами и лентами Мёбиуса.

Соединим плотно два обычных плоских кольца и запустим Эшеровского муравья ползать по внешней поверхности левого кольца. Когда он доползает до места соединения колец, то он может перебраться на внутреннюю поверхности второго кольца. Если же запустить второго муравья на внутреннюю поверхность левого кольца, то он может перебраться на внешнюю поверхность правого кольца. Иначе говоря, два эти муравья никогда не встретятся – каждый будет ползать по своей поверхности.

 

 

Понятно, что если таким образом построить цепь плоских колец или цепь из лент Мёбиуса, то эти свойства у них сохранятся.

С лентой Мёбиуса можно продолжить интересные эксперименты и дальше. Сделайте заготовку из листа бумаги, как показано на рисунке. Разрежьте по линиям, а затем каждую из получившихся полосочек, не отделенных от основной части, сверните в лист Мёбиуса. Получится этакая многоэтажная конструкция.

 

Конечно, на рисунке дано схематичное представление полученной структуры. Реальная «фракталообразная» фигуры такого типа выглядит гораздо более замысловато.

 

Вот по такому «кусту Мёбиуса» муравей бы вдосталь напутешествовался! Подобного рода многоярусных и вложенных друг в друга лент Мёбиуса можно понапридумать, конечно, очень много. 

В заключение приведем еще образец фигуры, которая обладает свойствами ленты Мёбиуса и при этом ни одна из сторон не скручена. Конечно, без маленьких хитростей дело не обошлось: попасть с внешней стороны на внутреннюю можно по «эскалатору» в центре кольца.

 

 

Очень легко подобного рода кольцо сделать даже с двумя эскалаторами, что обеспечит возможность муравью сделать полный цикл, не побывав ни разу в одной и той же точке (если, конечно, он не будет делать петель, а будет двигаться только вперед).